| 时间 | 备忘录 |
|---|---|
| 2024-11-11 | 开始阅读《深度学习的数学》 |
| 2024-11-19 | 第 1 章都是一些概念,每个概念都见过,组合在一起就看不太明白了。 |
| 2024-11-20 | 第 2 章的数学基础部分还好,很多知识点大学时都学过,也都知道。 今天把第 4 章看完了,信息量很大,大部分是浅尝辄止。 |
1 第 1 章:神经网络的思想
1.1 深度学习里的“深度”是什么意思呢?
1.2 神经网络的基本原理?
从数学上来说,其原理十分容易。本书的目的就是阐明它的原理。可能后面会解答清楚。
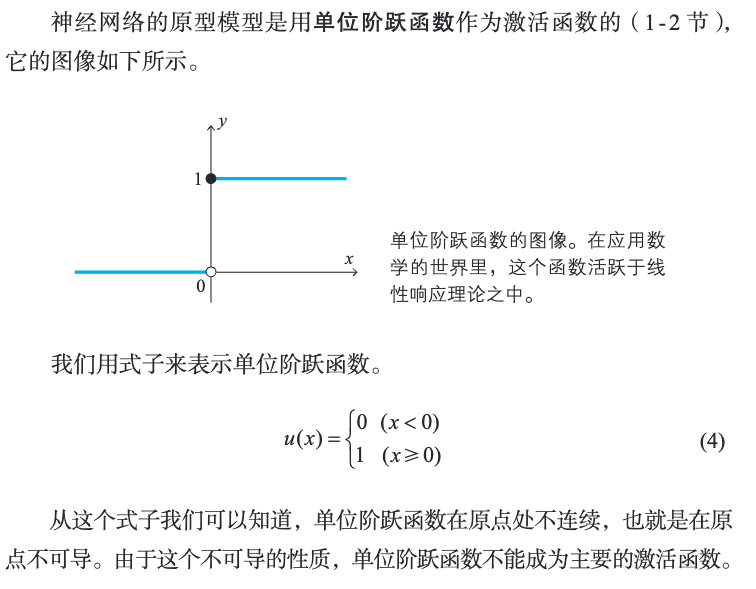
1.3 单位阶跃函数
单位阶跃函数,又称赫维赛德阶跃函数,通常用 H 或 θ 表记,有时也会用 u、 1 或 𝟙 表记,是一个由奥利弗·亥维赛提出的阶跃函数,参数为负时值为 0,参数为正时值为 1。分段函数形式的定义如下: 另一种定义为: 它是个不连续函数,其微分是狄拉克 δ 函数。
(深度学习的数学.pdf, p.10)
单位阶跃函数
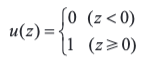
单位阶跃函数的图形如下所示:
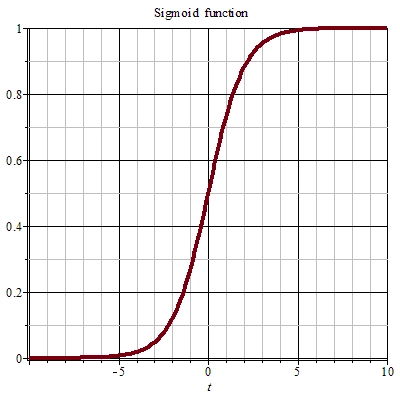
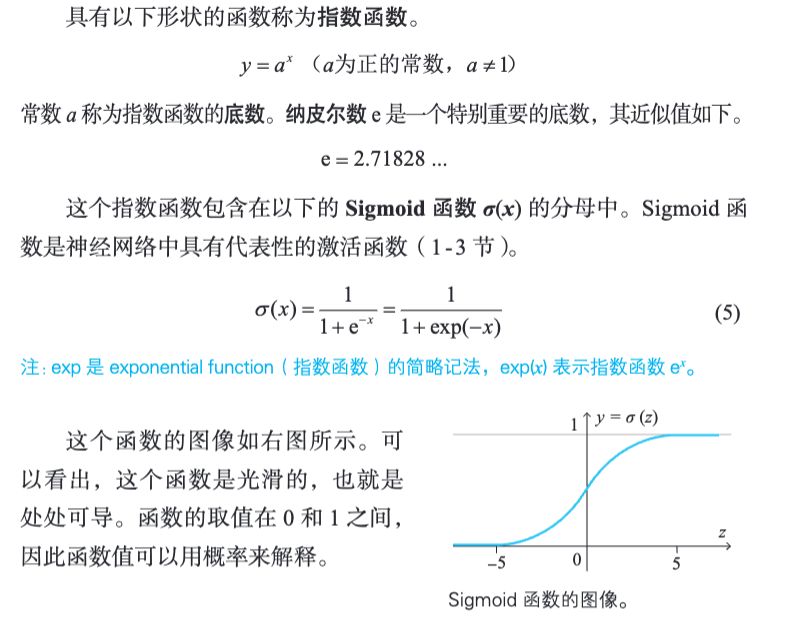
1.4 Sigmoid 函数
[!PDF|yellow] 深度学习的数学.pdf, p.11
Sigmoid 函数
S 型生长曲线。
Sigmoid 函数 也叫 Logistic 函数,用于隐层神经元输出,取值范围为 (0,1),它可以将一个实数映射到 (0,1) 的区间,可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。Sigmoid 函数为神经网络中的激励函数,是一种光滑且严格单调的饱和函数,其表达式为:
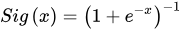
1.5 激活函数
在计算机网络中,一个节点的激活函数定义了该节点在给定的输入或输入的集合下的输出。
sigmoid 函数和 tanh 函数是研究早期被广泛使用的 2 种激活函数。两者都为 S 型饱和函数。当 sigmoid 函数输入的值趋于正无穷或负无穷时,梯度会趋近零,从而发生梯度弥散现象。Sigmoid 函数的输出恒为正值,不是以零为中心的,这会导致权值更新时只能朝一个方向更新,从而影响收敛速度。Tanh 激活函数是 sigmoid 函数的改进版,是以零为中心的对称函数,收敛速度快,不容易出现 loss 值晃动,但是无法解决梯度弥散的问题。2 个函数的计算量都是指数级的,计算相对复杂。Softsign 函数是 tanh 函数的改进版,为 S 型饱和函数,以零为中心,值域为(−1,1)。
[!PDF|yellow] 深度学习的数学.pdf, p.12
激活函数:将神经元的工作一般化

[!PDF|yellow] 深度学习的数学.pdf, p.14
激活函数的代表性例子是 Sigmoid 函数 σ(z)
1.6 权重
激活函数中对应的输入信号的系数。
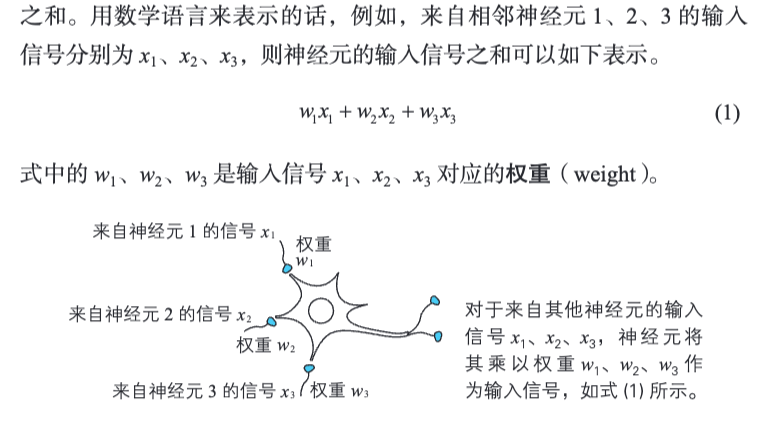
对应到神经网络中就量,每层神经元传递信号时的系数。
1.7 权重的大小如何确定呢?
[!PDF|yellow] 深度学习的数学.pdf, p.36
神经网络中比较重要的一点就是利用网络自学习算法来确定权重大小。
1.8 逻辑回归
logistic 回归是一种广义线性回归(generalized linear model),因此与多重线性回归分析有很多相同之处。
1.9 自变量、因变量
广义解释任何一个系统(或模型)都是由各种变量构成的,当分析这些系统(或模型)时,可以选择研究其中一些变量对另一些变量的影响,那么选择的这些变量就称为自变量,而被影响的量就被称为因变量。例如:分析人体这个系统中,呼吸对于维持生命的影响,那么呼吸就是自变量,而生命维持的状态被认为是因变量。
1.10 偏置
我们将 - θ 替换为 b。
[!PDF|yellow] 深度学习的数学.pdf, p.16
经过这样处理,式子变漂亮了,也不容易发生计算错误。这个 b 称为偏置(bias)
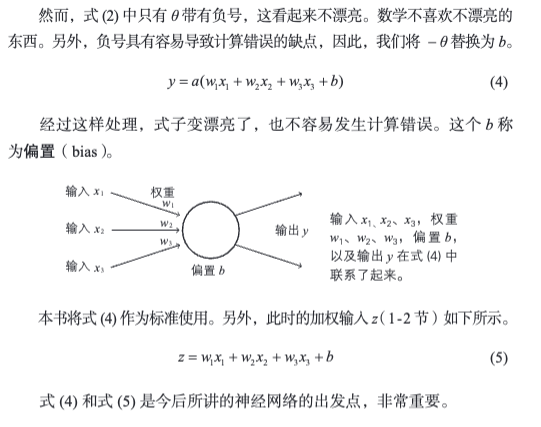
卧槽,为了变漂亮搞这么一手?
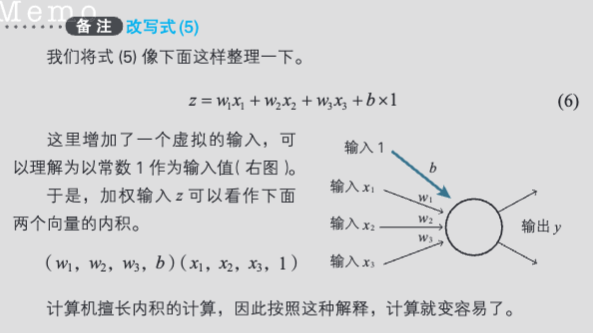
1.11 内积
在数学 中,点积(德语:Punktprodukt;英语:dot product)又称数量积或标量积(德语:Skalarprodukt;英语:scalar product),是一种接受两串等长的数字序列(通常是坐标向量)、返回单一数字的代数运算。
在欧几里得几何 里,两条笛卡尔坐标 向量的点积常称为内积(德语:inneres Produkt;英语:inner product)。点积是内积的一种特殊形式:内积是点积的抽象,内积是一种双线性函数,点积是欧几里得空间(内积空间)的度量。
从代数角度看,先求两数字序列中每组对应元素的积,再求所有积之和,结果即为点积。从几何角度看,点积则是两向量的长度 与它们夹角余弦 的积。这两种定义在笛卡尔坐标系中等价。
点积的名称源自表示点乘运算的点号(a⋅b 
a dot b,标量积的叫法则是在强调其运算结果为标量 而非向量。向量的另一种乘法是**叉乘(a×b 
a cross b,其结果为向量,称为叉积或向量积**。
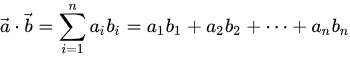
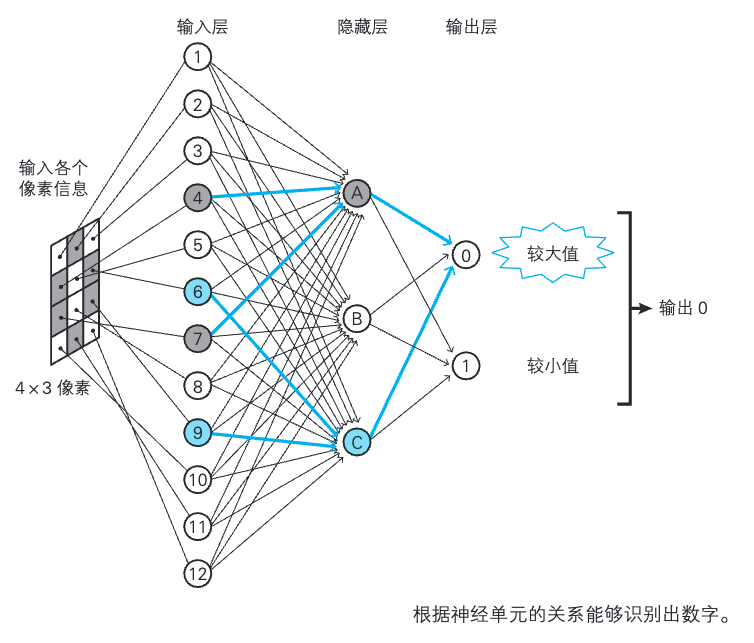
1.12 什么是神经网络?
神经元连接成网络。神经网络是将神经单元部署成网络状而形成的。
[!PDF|yellow] 深度学习的数学.pdf, p.18
将这样的神经单元连接为网络状,就形成了神经网络。
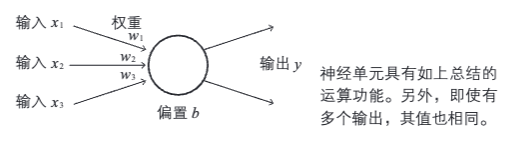
[!PDF|yellow] 深度学习的数学.pdf, p.19
网络的连接方法多种多样,本书将主要考察作为基础的阶层型神经网络以及由其发展而来的卷积神经网络。
1.13 神经网络各层的职责
主要针对阶层型神经网络。输入层、隐藏层、输出层。其中
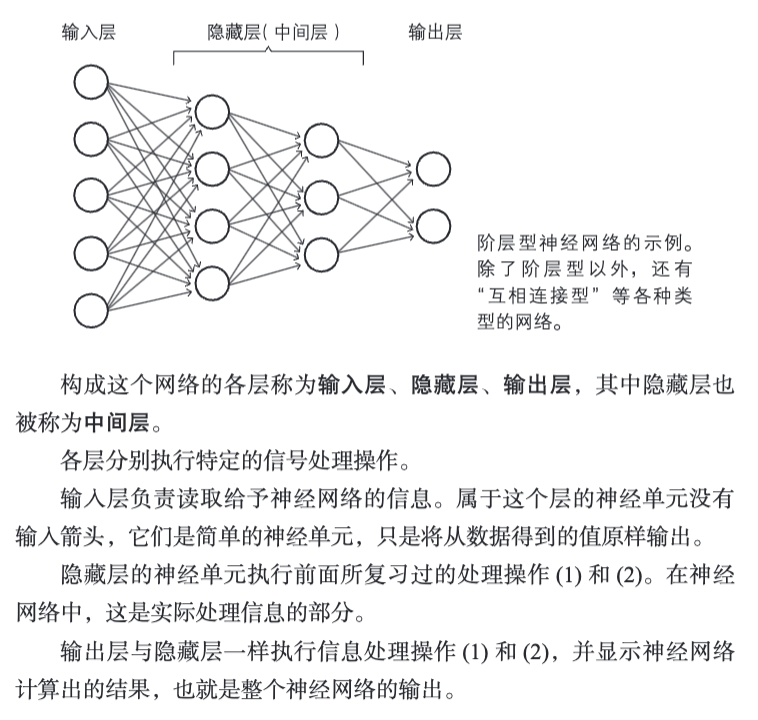
其中,(1)(2)对应:

1.14 什么是深度学习?
[!PDF|yellow] 深度学习的数学.pdf, p.20
深度学习,顾名思义,是叠加了很多层的神经网络。叠加层有各种各样的方法,其中著名的是卷积神经网络
1.15 全连接层(fully connected layer)
[!PDF|yellow] 深度学习的数学.pdf, p.21
前一层的神经单元与下一层的所有神经单元都有箭头连接,这样的层构造称为全连接层(fully connected layer)
1.16 隐藏层的作用?
- 为何能够提取输入图像的特征呢?
- 隐藏层设置为几层比较好?
它很重要,这是多层神经网络中最维的部分。支撑整个神经网络工作的就是这个隐藏层。
[!PDF|yellow] 深度学习的数学.pdf, p.22
隐藏层具有提取输入图像的特征的作用。
[!PDF|yellow] 深度学习的数学.pdf, p.23
隐藏层肩负着特征提取(feature extraction)的重要职责
1.17 消除噪声处理?
就是前面提到的偏置。
- 大家说的调参,是它么?
[!PDF|yellow] 深度学习的数学.pdf, p.29
具体来说,将偏置放在恶魔的心中,以忽略少量的噪声。这个“心的偏置”是各个恶魔固有的值 (也就是个性)
1.18 恶魔之间的“交情”表示权重。心的偏置?恶魔的工作?
这就是 “由神经网络中的关系得出答案”的思想。
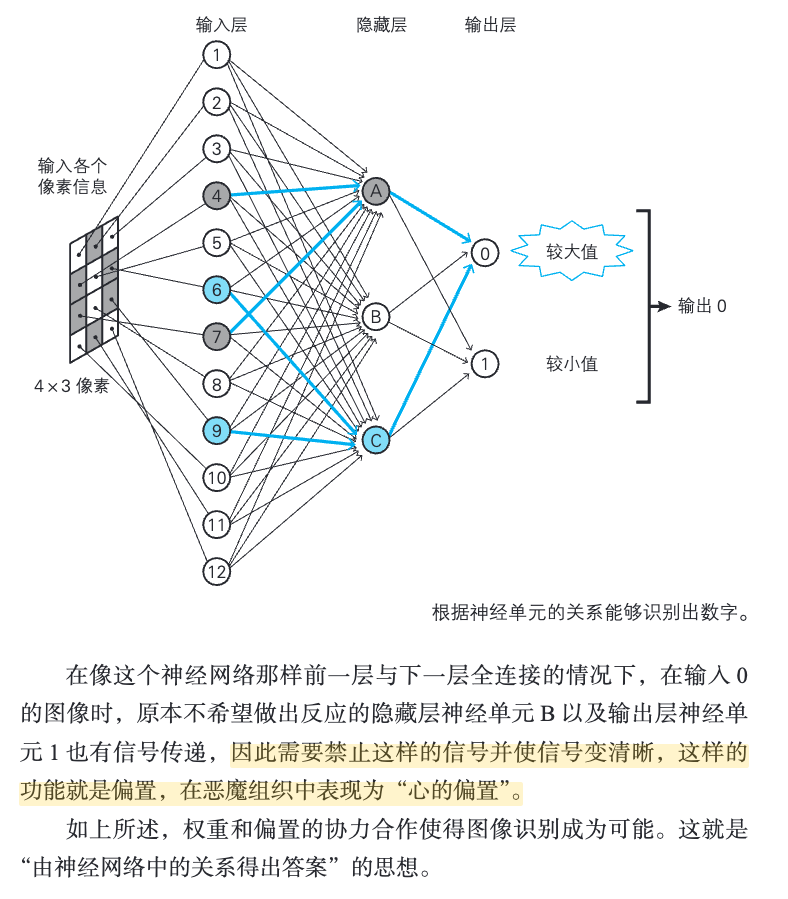
[!PDF|yellow] 深度学习的数学.pdf, p.33
因此需要禁止这样的信号并使信号变清晰,这样的功能就是偏置,在恶魔组织中表现为“心的偏置”
1.19 模型的合理性
求解出多层神经网络实现工作权重和偏置。
[!PDF|yellow] 深度学习的数学.pdf, p.34
并能够充分地解释所给出的数据,就能够验证以上话题的合理性。这需要数学计算,必须将语言描述转换为数学式。
1.20 隐藏层需要多少个神经元?
书中说,存在某种预估?
这个就有有点玄学了啊!规模大的时候如何估呢!?
- 关于具体的确认方法,将在第 3 章解答。
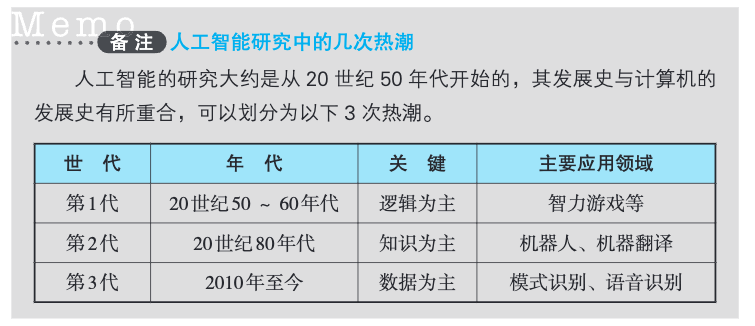
1.21 人工智能研究中的几次热潮
1.22 神经网络参数确定的方法
[!PDF|yellow] 深度学习的数学.pdf, p.36
神经网络的参数确定方法分为有监督学习和无监督学习。
1.23 学习数据
[!PDF|yellow] 深度学习的数学.pdf, p.36
有监督学习是指,为了确定神经网络的权重和偏置,事先给予数据,这些数据称为学习数据
1.24 学习
[!PDF|yellow] 深度学习的数学.pdf, p.36
根据给定的学习数据确定权重和偏置,称为学习。注:学习数据也称为训练数据。
1.25 最优化
[!PDF|yellow] 深度学习的数学.pdf, p.36
神经网络是怎样学习的呢?思路极其简单:计算神经网络得出的预测值与正解的误差,确定使得误差总和达到最小的权重和偏置。这在数学上称为模型的最优化
1.26 代价函数(cost function)
用符号 CT 表示(T 是 Total 的首字母)。
[!PDF|yellow] 深度学习的数学.pdf, p.36
关于预测值与正解的误差总和,有各种各样的定义。本书采用的是最古典的定义:针对全部学习数据,计算预测值与正解的误差的平方(称为平方误差),然后再相加。这个误差的总和称为代价函数(cost function)
1.27 最小二乘法
- 我们将在 2 - 12 节以回归分析为例来具体考察什么是最小二乘法。
[!PDF|yellow] 深度学习的数学.pdf, p.36
利用平方误差确定参数的方法在数学上称为最小二乘法,它在统计学中是回归分析的常规手段。
2 第 2 章:神经网络的数学基础
2.1 一次函数

[!PDF|yellow] 深度学习的数学.pdf, p.41
神经单元的加权输入可以表示为一次函数关系

2.2 二次函数

2.3 单位阶跃函数
2.4 指数函数与 Sigmoid 函数
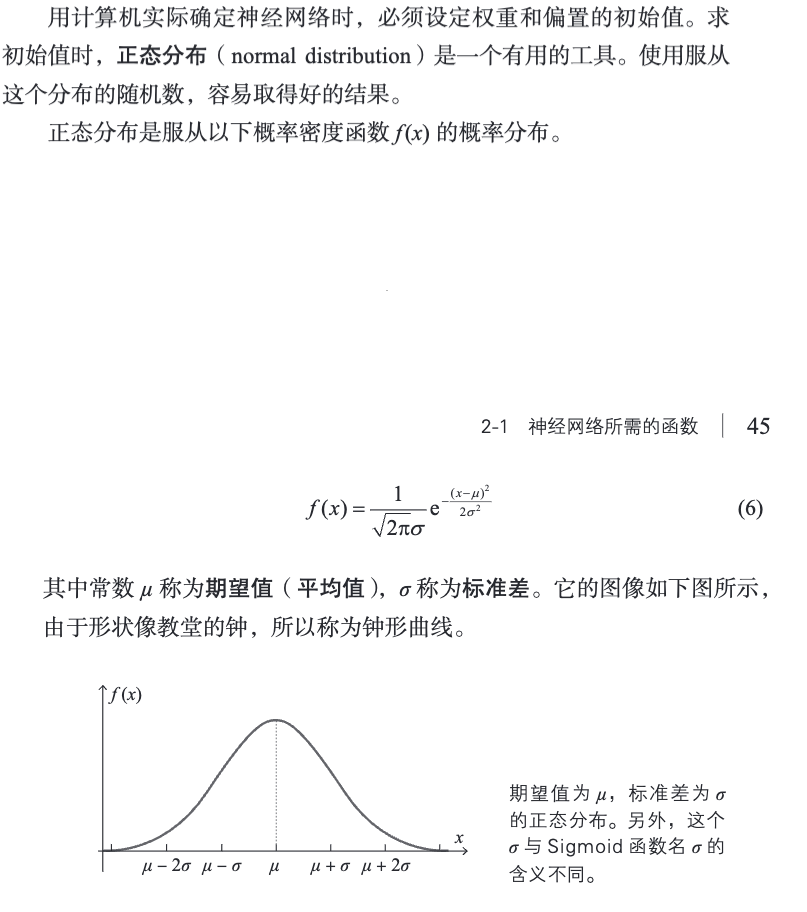
2.5 正态分布的概率密度函数
2.6 数列
[!PDF|yellow] 深度学习的数学.pdf, p.46
在神经网络的世界中出现的数列是有限项的数列。这样的数列称为有穷数列。在有穷数列中,数列的最后一项称为末项。
2.7 数列的通项公式
[!PDF|yellow] 深度学习的数学.pdf, p.47
将数列的第 n 项用一个关于 n 的式子表示出来,这个式子就称为该数列的通项公式。


2.8 递推关系式
即,数列的递推公式。
2.9 向量
[!PDF|yellow] 深度学习的数学.pdf, p.54
把向量的箭头放在坐标平面上,就可以用坐标的形式表示向量。把箭头的起点放在原点,用箭头终点的坐标表示向量,这叫作向量的坐标表示。
[!PDF|yellow] 深度学习的数学.pdf, p.55
从直观上来讲,表示向量的箭头的长度称为这个向量的大小。
向量的内积:
2.10 柯西-施瓦茨不等式

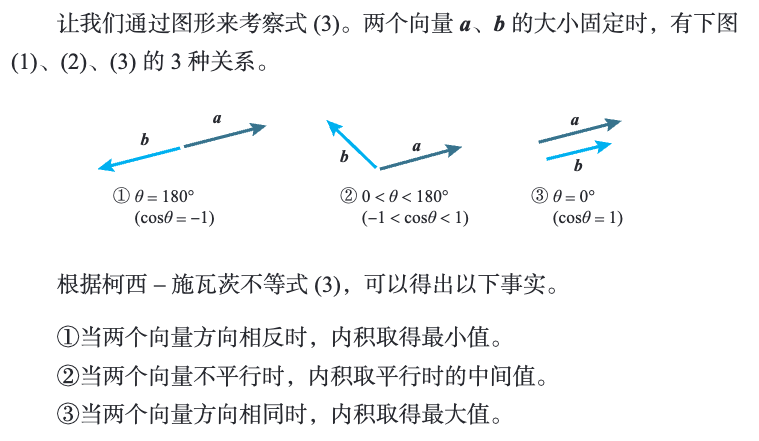
- 性质 ① 就是后述的梯度下降法的基本原理。
- 后面我们考察卷积神经网络时,这个观点就变得十分重要(附录 C)。
2.11 矩阵
[!PDF|yellow] 深度学习的数学.pdf, p.63
矩阵的乘法不满足交换律
[!PDF|yellow] 深度学习的数学.pdf, p.63
而单位矩阵 E 与任意矩阵 A 的乘积都满足以下交换律
转置矩阵。
2.12 Hadamard 乘积
在数学中,**阿达马矩阵(英语:Hadamard matrix**)是一种特殊的正交矩阵,具有一些重要的性质和应用。它的特点是每个元素只能是+1 或-1,并且每行(或每列)之间的内积为 0,表示彼此正交。Hadamard 矩阵的大小为 2 的幂次方,即维度为 
阿达马矩阵常用于纠错码,如 Reed-Muller 码。阿达马矩阵的命名来自于法国数学家雅克·阿达马。
2.13 导数
[!PDF|yellow] 深度学习的数学.pdf, p.69
当函数 f (x) 在 x = a 处取得最小值时,f’ (a) = 0。
[!PDF|yellow] 深度学习的数学.pdf, p.69
f’ (a) = 0 是函数 f (x) 在 x = a 处取得最小值的必要条件。
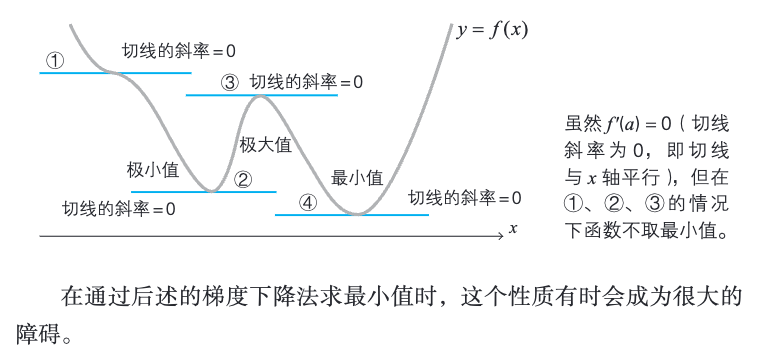
2.14 偏导数基础
[!PDF|yellow] 深度学习的数学.pdf, p.72
本节我们来考察有两个以上的自变量的函数。有两个以上的自变量的函数称为多变量函数。
[!PDF|yellow] 深度学习的数学.pdf, p.73
关于某个特定变量的导数就称为偏导数(partial derivative)

2.15 多变量函数的最小值条件
[!PDF|yellow] 深度学习的数学.pdf, p.74
光滑的单变量函数 y = f (x) 在点 x 处取得最小值的必要条件是导函数在该点取值 0

2.16 拉格朗日乘数法
λ:拉姆达

2.17 复合函数

2.18 复合函数求导公式
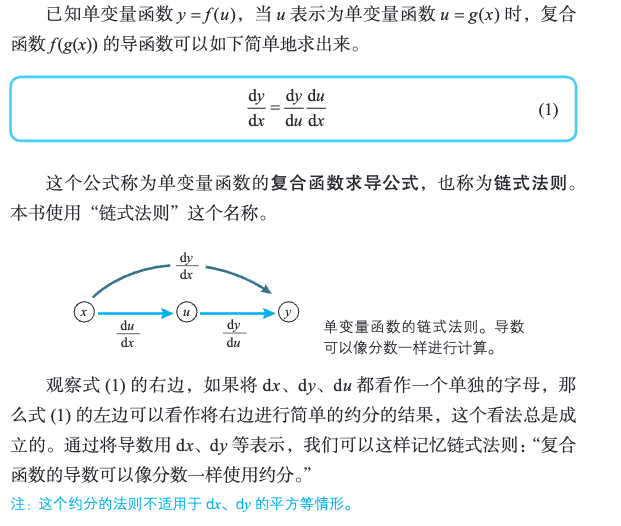
2.19 多变量函数的近似公式


2.20 梯度下降法的含义与公式
[!PDF|yellow] 深度学习的数学.pdf, p.84
在数值分析领域,梯度下降法也称为最速下降法。

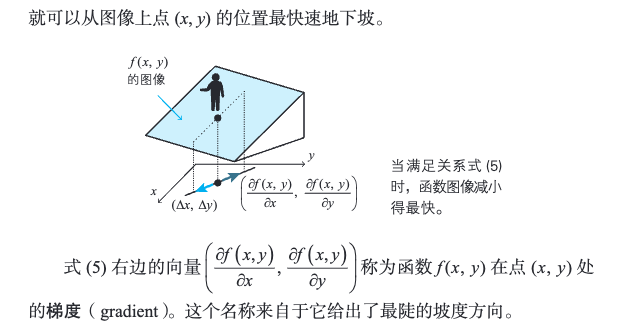
[!PDF|yellow] 深度学习的数学.pdf, p.88
这种寻找函数 f (x, y) 的最小值点的方法称为二变量函数的梯度下降法。
2.21 哈密顿算子 ∇
[!PDF|yellow] 深度学习的数学.pdf, p.89
∇ 称为哈密顿算子

2.22 梯度下降法的要点
[!PDF|yellow] 深度学习的数学.pdf, p.90
η 只是简单地表示正的微小常数。而在实际使用计算机进行计算时,如何恰当地确定这个 η 是一个大问题。
[!PDF|yellow] 深度学习的数学.pdf, p.90
在神经网络的世界中,η 称为学习率。遗憾的是,它的确定方法没有明确的标准,只能通过反复试验来寻找恰当的值。
2.23 最优化问题
[!PDF|yellow] 深度学习的数学.pdf, p.94
在为了分析数据而建立数学模型时,通常模型是由参数确定的。在数学世界中,最优化问题就是如何确定这些参数。
从数学上来说,确定神经网络的参数是一个最优化问题,具体就是对神经网络的参数(即权重和偏置)进行拟合,使得神经网络的输出与实际数据相吻合。
为了理解最优化问题,最浅显的例子就是回归分析。
2.24 回归分析
[!PDF|yellow] 深度学习的数学.pdf, p.94
由多个变量组成的数据中,着眼于其中一个特定的变量,用其余的变量来解释这个特定的变量,这样的方法称为回归分析。
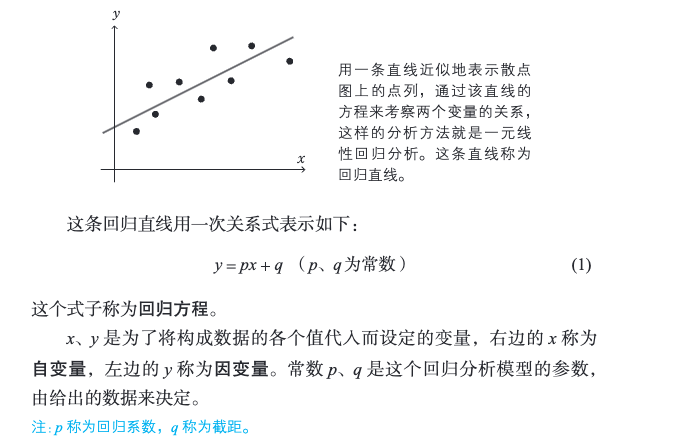
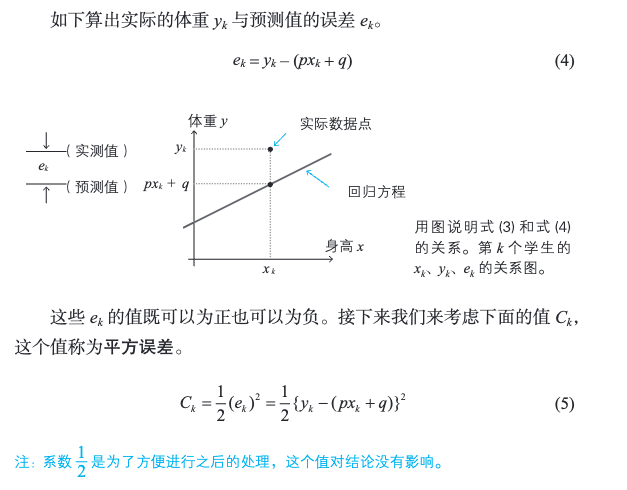

回归分析认为,p、q 是使误差总和式 (6) 最小的解。接下来求偏导就行了。
2.25 代价函数(损失函数)
[!PDF|yellow] 深度学习的数学.pdf, p.98
在最优化方面,误差总和 CT 可以称为“误差函数”“损失函数”“代价函数”等。本书采用代价函数(cost function)这个名称。
[!PDF|yellow] 深度学习的数学.pdf, p.98
利用平方误差的总和 CT 进行最优化的方法称为最小二乘法。本书中我们只考虑将平方误差的总和 CT 作为代价函数。
2.26 模型参数的个数
[!PDF|yellow] 深度学习的数学.pdf, p.99
回归方程是根据大量的条件所得到的折中结果。这里所说的“折中”是指,理想中应该取值 0 的代价函数式 (6) 只能取最小值。因此,模型与数据的误差 CT 不为 0 也无须担心。不过,只要误差接近 0,就可以说这是合乎数据的模型。
3 神经网络的最优化
3.1 参数和变量
[!PDF|yellow] 深度学习的数学.pdf, p.102
像权重和偏置这种确定数学模型的常数称为模型的参数。
[!PDF|yellow] 深度学习的数学.pdf, p.103
首先,我们对层进行编号,如下图所示,最左边的输入层为层 1,隐藏层(中间层)为层 2、层 3……最右边的输出层为层 l(这里的 l 指 last 的首字母,表示层的总数)。
注意:权重 w 的下标表示。
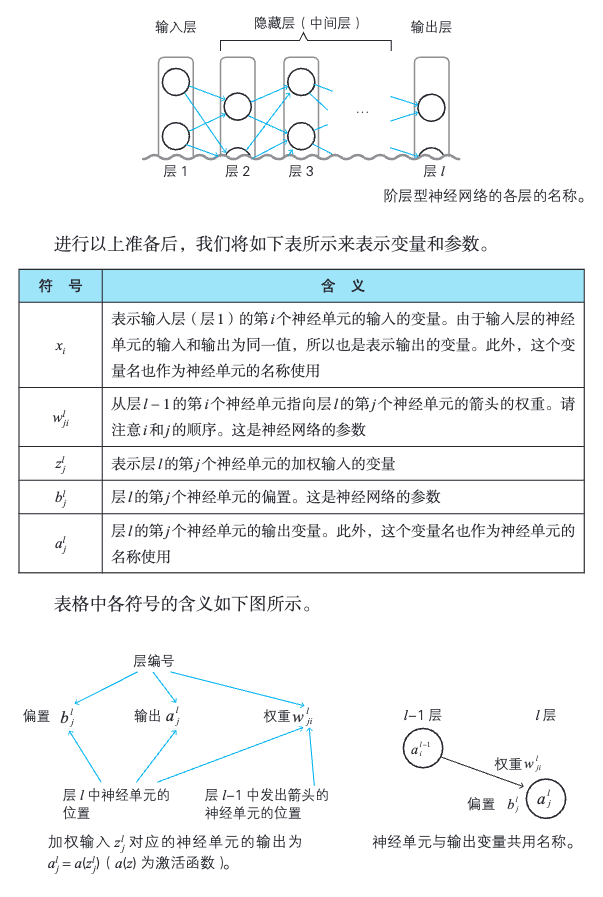
[!PDF|yellow] 深度学习的数学.pdf, p.107
变量值的表示方法

3.2 神经网络的变量的关系式


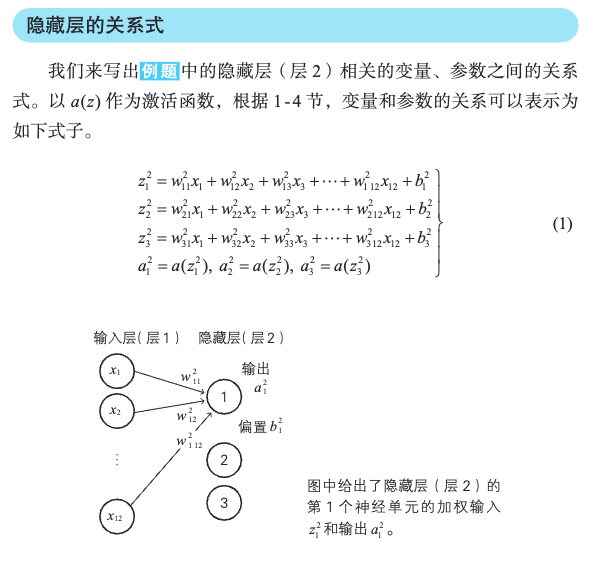

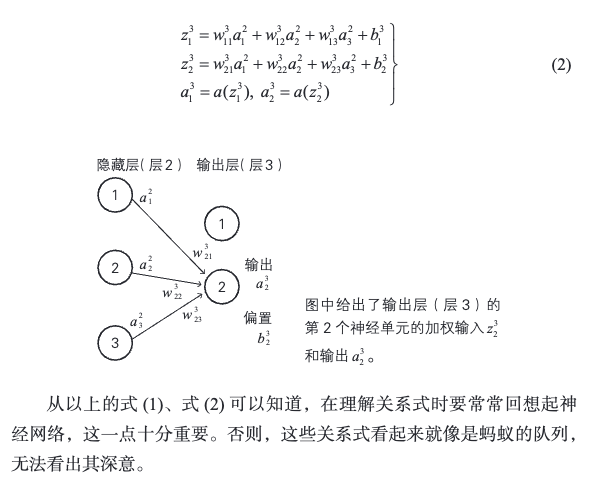
[!PDF|yellow] 深度学习的数学.pdf, p.113
神经网络的变量的矩阵表示
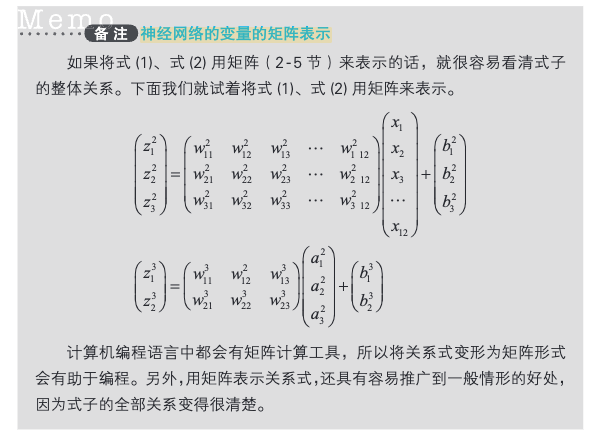
3.3 神经网络的学习数据和正解
[!PDF|yellow] 深度学习的数学.pdf, p.114
利用事先提供的数据(学习数据)来确定权重和偏置,这在神经网络中称为学习(1 - 7 节)。学习的逻辑非常简单,使得神经网络算出的预测值与学习数据的正解的总体误差达到最小即可。
[!PDF|yellow] 深度学习的数学.pdf, p.115
经网络的情况下,则通常无法将预测值和正解整合在一张表里。
[!PDF|yellow] 深度学习的数学.pdf, p.116
如何将这些正解教给神经网络呢?
[!PDF|yellow] 深度学习的数学.pdf, p.116
神经网络的预测值用输出层神经单元的输出变量来表示。
加正解变量:
[!PDF|yellow] 深度学习的数学.pdf, p.117
那么如何将 1 个正解和 2 个输出变量对应起来呢?
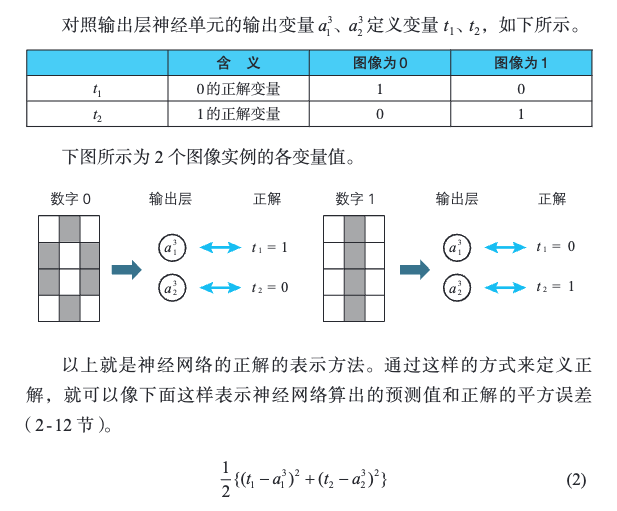
3.4 交叉熵

3.5 最优化
[!PDF|yellow] 深度学习的数学.pdf, p.119
用于数据分析的数学模型是由参数确定的。在神经网络中,权重和偏置就是这样的参数。通过调整这些参数,使模型的输出符合实际的数据(在神经网络中就是学习数据),从而确定数学模型,这个过程在数学上称为最优化(2 - 12 节),在神经网络的世界中则称为学习(1 - 7 节)。
[!PDF|yellow] 深度学习的数学.pdf, p.119
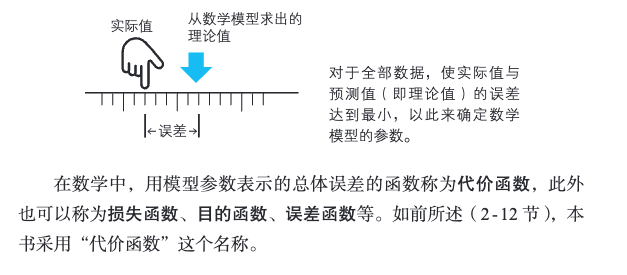
参数是怎样确定的呢?其原理非常简单,具体方法就是,对于全部数据,使得从数学模型得出的理论值(本书中称为预测值)与实际值的误差达到最小。
4 第 4 章:神经网络和误差所向传播法
4.1 函数最小值
[!PDF|yellow] 深度学习的数学.pdf, p.134
求函数最小值的通用方法中,最有名的就是利用最小值条件。

但是,在规模比较大的时候方程会很多,求解方程极其困难。于是,梯度下降法应运而生。
4.2 在神经网络中应用梯度下降法

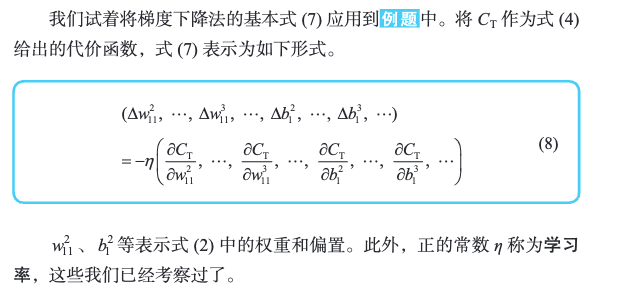
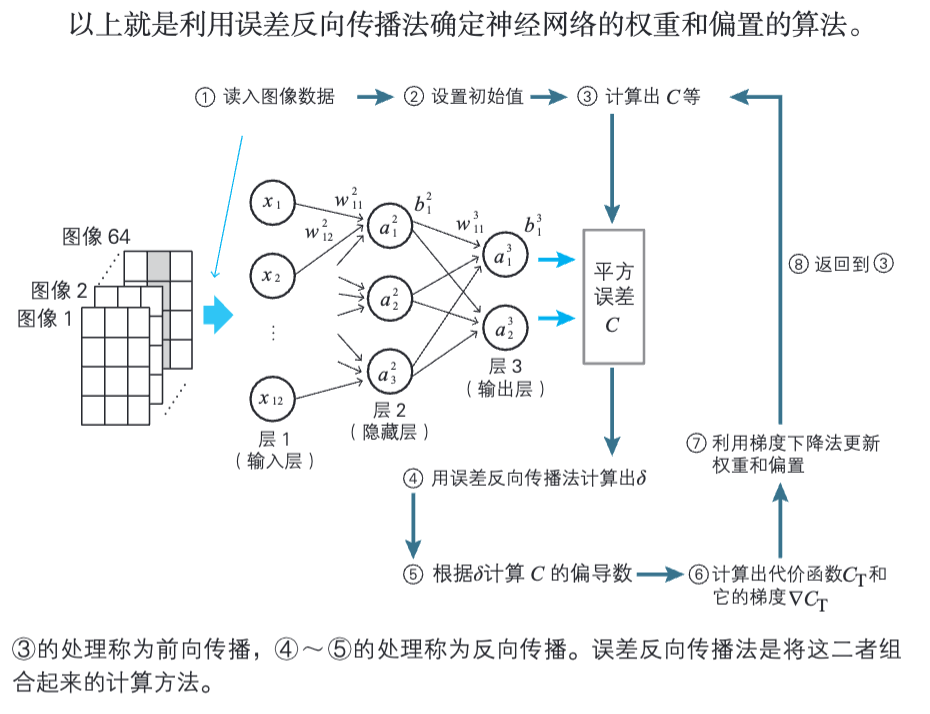
梯度下降虽然香,但是对平方误差求导却很麻烦。于是,有了误差所向传播法。
[!PDF|yellow] 深度学习的数学.pdf, p.139
用具体的式子来求梯度分量是一件非常困难的工作。虽然单个的计算比较简单,但是会被导数的复杂与繁多所压倒,进入所谓“导数地狱”的世界。为了解决这个问题,人们研究出了误差反向传播法。
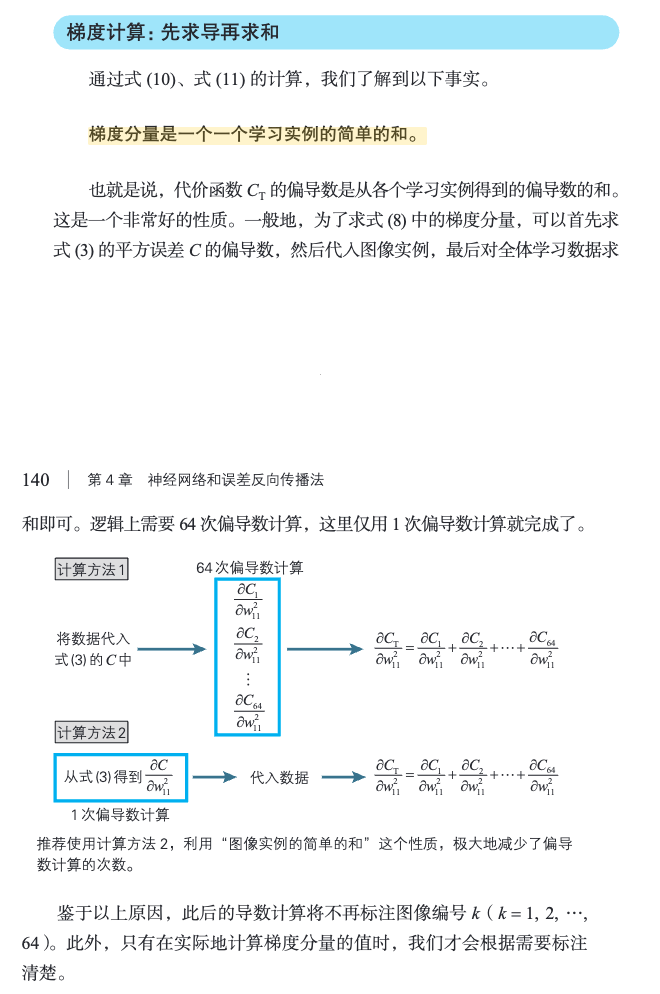
先求导再求和:
[!PDF|yellow] 深度学习的数学.pdf, p.139
梯度分量是一个一个学习实例的简单的和。
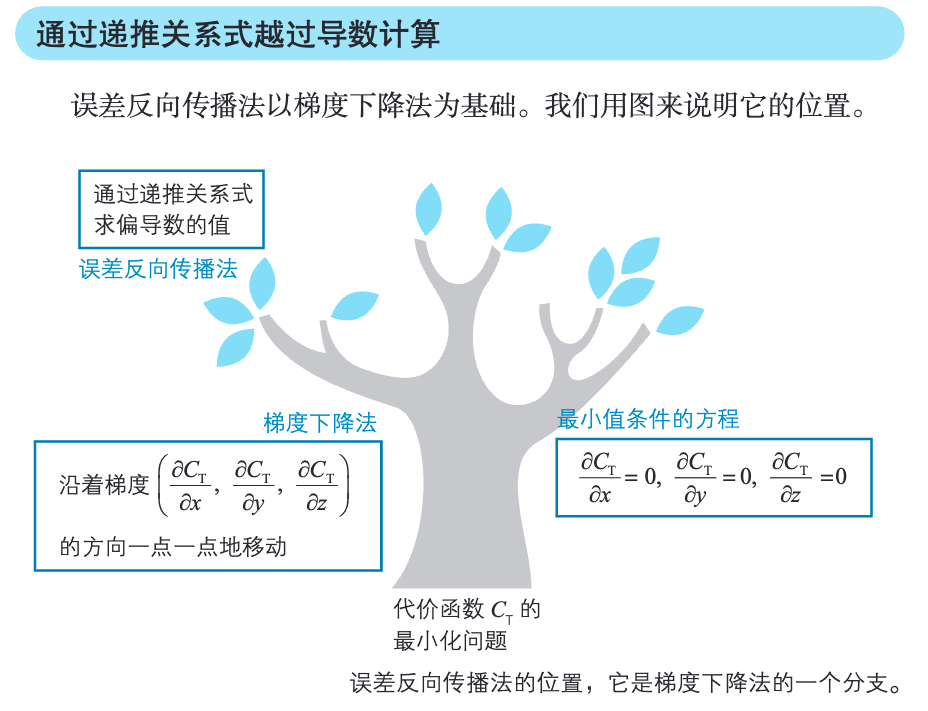
4.3 误差反向传播法(BP 法)

[!PDF|yellow] 深度学习的数学.pdf, p.141
梯度下降法对于寻找多变量函数的最小值的问题是有效的。然而在神经网络的世界中,变量、参数和函数错综复杂,无法直接使用梯度下降法,于是就出现了误差反向传播法。
[!PDF|yellow] 深度学习的数学.pdf, p.146
误差反向传播法的特点是将繁杂的导数计算替换为数列的递推关系式。
4.4 神经单元误差


[!PDF|yellow] 深度学习的数学.pdf, p.148
如果给出平方误差 C 和激活函数,就可以具体地求出相当于“末项”的输出层神经单元误差
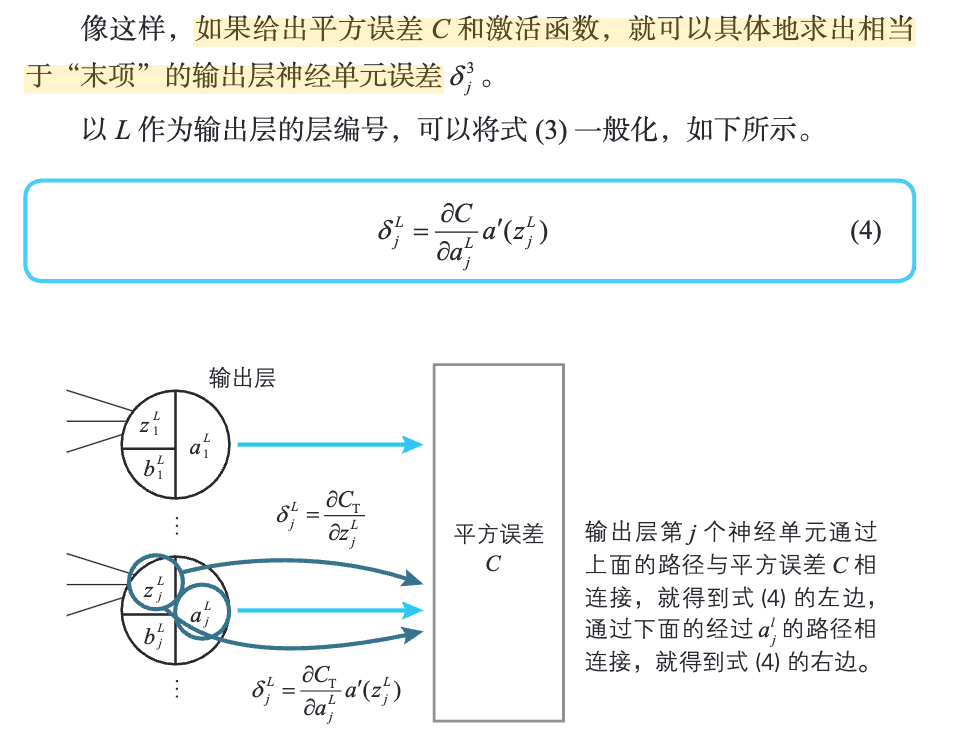

4.5 反向传播算法计算神经网络的权重和偏置

- 4-1 节式(2):

- 4-1 节式(3):

- 层的神经网络误差计算:

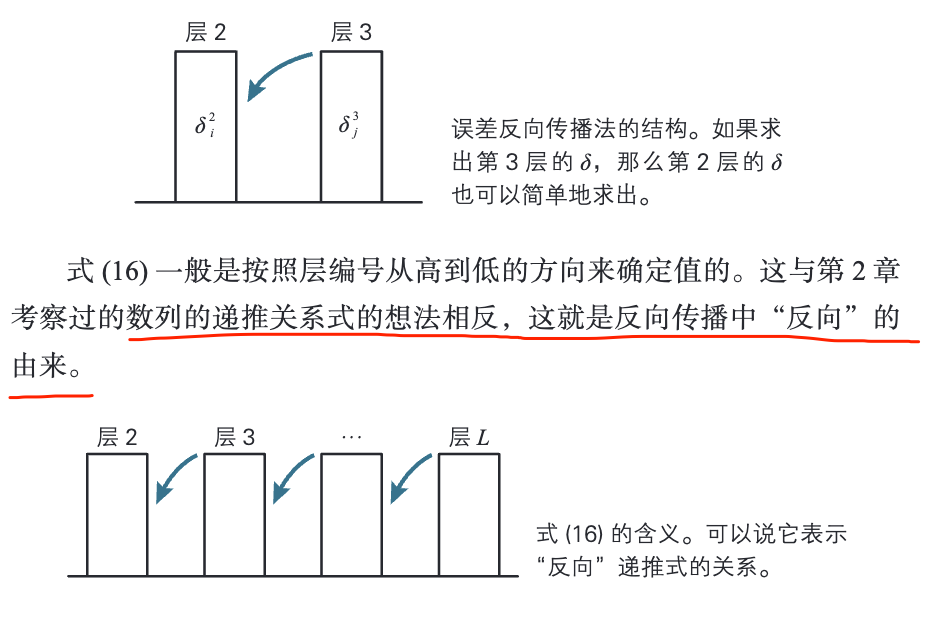
- 4-3 节式(16):

- 4-1 节式(9):

- 4-2 节式(11):

5 第 5 章:深度学习和卷积神经网络
5.1 神经网络的结构
[!PDF|yellow] 深度学习的数学.pdf, p.168
图中用圆圈将变量名圈起来的就是神经单元,从这个图中我们可以了解到卷积神经网络的特点。隐藏层由多个具有结构的层组成。具体来说,隐藏层是多个由卷积层和池化层构成的层组成的。它不仅“深”,而且含有内置的结构。
5.2 卷积层
[!PDF|yellow] 深度学习的数学.pdf, p.168
卷积层的英文是 convolution layer。
- 什么是卷积?